EME Echo Doppler Spreading and Lunar Libration

When an EME signal is reflected from the moon, what does it look like? Below are there representations on how the signal might look.

  

On the left is what the reflected power distribution would look like of the moon was a flat 2 dimensional disk. Equal power would be reflected back from all parts of the disk. But the moon is a sphere, not a disk, and the center shows what the power distribution would be if the moon was highly reflective sphere. There would be a small, bright reflection from the center and nothing else. But the moon isn't a highly reflective sphere either. Finally the image on the left shows the reflected power distribution from a matte sphere. Most of the power is reflected from the center of the visible face of the sphere, but there is some power reflected from all parts, with decreasing power as the reflection moves to the edge.

So what about the real moon? Well the reflected power distribution depends somewhat on the wavelength of the signal being reflected. On the lower bands much of the reflected power comes from the center of the visible "disk", but on the higher bands the reflected power distribution is more like that of the matte surface. Another way of saying this is that reflection is always something of a mixture of specular and diffuse (matte) reflection, which a bias a little towards specular reflection at lower frequencies (e.g. 144/432) and slightly towards a diffuse reflection at higher frequencies(e.g 10/24 GHz).

So why does this matter and what does it have to do with Doppler Spreading and Lunar Libration?

Doppler Spreading

A Doppler shift is observed if the object a signal is reflected has some component of notion either towards of away from the observer. So the reflection from a rotating sphere will show different Doppler shifts depending on which part of the sphere the signal is reflected from. Take the following example:

Here we are looking at a sphere at a constant distance, rotating about a vertical axis with the right side rotating towards the observer and the left side rotating away (clockwise rotation as seen from above). Signals reflecting from a strip between the "north" and "south" poles and passing through the center of the visible disk will have no component of motion towards or away from the observer, so have no Doppler shift. However signals reflected from the left side of the "disk" (which is moving away) will shift to lower frequency ("red shift"), and the magnitude of the shift will increase as you move out from the center to the edge. Similarly, the right side of the "disk" is moving towards the observer and so they will see an increase in frequency ("blue-shift").

The result of all this is that a single frequency is broadened when reflected from a rotating sphere. It comes back as a band of frequencies rather than a single frequency as shown below:

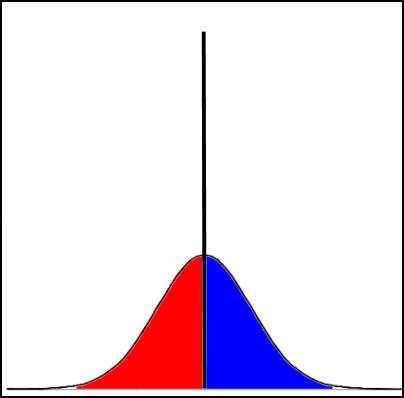
The initial single frequency spreads out, with the red-shifted components on one side and the blue shifted components on the other.

The Moon

The simple view of the moon is that it always keeps the same face when viewed from the earth, i.e. from the point of view of an observer on the surface of the earth, the moon does not rotate. However, this simple view isn't correct. Due to the complexities of the orbital motions of the earth-moon system, the moon does, in fact, appear to rotate about various axes. The motion is complex, but can be calculated and a simulation of what we actually see is shown in the video below. The simple model would predict we would be able to see only 50% of the surface of the moon. In fact, due to libration, be can see about 59%. Wikipedia describes Libration as "... libration is the wagging or wavering of the Moon perceived by Earth-bound observers and caused by changes in their perspective. It permits an observer to see slightly different hemispheres of the surface at different times..."

Why does Doppler Broadening matter?

Doppler broadening (a consequence of libration) matters because as the echo broadens,the signal to noise ratio goes down, and that makes the signal harder to detect and thus, if a digital signal, harder to decode. If we assume a background of uniform noise, the total power of that noise is proportional to the bandwidth it is measured in. There is twice as much noise (3dB more) in a 40Hz bandwidth that there is in a 20Hz bandwidth, and twice as much noise (3dB more) in a 20Hz bandwidth as in a 10 Hz bandwidth. So if we look at the entire signal and that signal has a S/N ratio of -10dB and is 10 Hz wide, if it spreads to 20Hz, the S/N ratio will be -13dB, and if it spreads to 40Hz, the S/N ratio will be -16dB.

When Doppler broadening (libration spreading) is low, it's possible to use narrower band digital modes (E.g JT65A rather than JT65B or JT65C). The narrower modes are capable of decoding weaker signals. You can't use them all the time because using a very narrow mode on a widely spread signal results in the inability to separate the individual tones of the digitally encode message. If the tones are spaced 2Hz apart and each tone is spread out by 20Hz, the difficulty of detecting individual tones is obvious.