Estimating Gain loss due to pointing error - off axis dish gain

When planning an EME system it can be useful to know just how accurately the antenna needs to be pointed in order to minimize any gain loss due to pointing error. To do this accurately you would need to know the beam pattern of the antenna which could either be measured or modeled. Modeling is beyond the capabilities of most amateurs and measuring is difficult, even if you have the antenna you are intending to use.

So is there a way to estimate the off-axis gain of an antenna? The answer is yes, especially for a parabolic dish and feed system commonly used for EME work. I dish usually has a fairly symmetrical and predictable main lobe pattern. The shape of the main lobe pattern (certainly out to the -3dB points, maybe out to the -10dB point) can be approximated by a Gaussian curve as in the example below, which is for the "close to axis" region of the main lobe of an antenna with a -3dB beamwidth of 5 degrees.

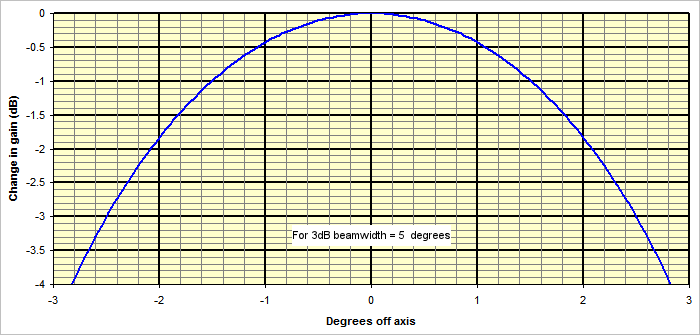
The (Gaussian) shape of the curve is the same for all beamwidths, so the same plot can be used for any beamwidth by appropriately scaling the X axis. To find the gain loss for an antenna with a 3dB beamwidth of 2 degrees when the pointing error was 0.5 degrees, you'd look at the loss corresponding to a value of 0.5 * (5/2) = 1.25 on the x-axis, which is around 0.7dB.

The shape of the main lobe is affected by changes in how the dish is illuminated (i.e. the feed pattern) and this is discussed in John Krause's book "Radio Astronomy" (specifically in figure 6-9 and appendix 6), but for our purposes, with feeds used for EME, the Gaussian shape is a good enough approximation.

There are a number of simple relationship between peak gain, the beamwidth at the -3dB point and the off axis gain of the main lobe which don't require calculating a Gaussian curves or the full theoretical antenna pattern.

(1) Estimating the -3dB beamwidth

The full beamwidth at the -3dB points of a dish can be approximated using the relationship

3dB Beamwidth (degrees) = 70 * (Wavelength/Diameter)       {1}

So for a 3m dish at 1296MHz (23.14cm wavelength), the 3dB beamwidth would be 70 * (23.14/300) = 5.4 degrees

(2) Estimate the off-axis gain ) gain loss due to pointing error)

Once you have the -3dB beamwidth you can use the following relationship to estimate the off axis gain loss:

Off Axis Gain Loss (dB) = 12 * (off_axis_angle/3dB-beamwidth)^2       {2}

So, for the 3m dish on 1296MHz with a 3dB beamwidth of 5.4 degrees, if we want to know the loss in gain for a 1 degree pointing error, the answer is:

Gain loss for 1 degree off axis = 12 * (1/5.4)^2 = 12 * 0.0343 = 0.41dB

If you want to know how far off axis you need to be for a given gain loss, you can rearrange the expression to give you:

Off_axis_angle = SQRT [(Gain_loss * 3dB_beamwidth^2)/12]       {2a}

So if we have the same 3m dish on 1296 and we want to know the pointing error that will result in a 1dB loss of gain, this can be estimated by:

Off_axis_angle = SQRT [(1*5.4^2)/12] = SQRT [2.43] = 1.56 degrees

(3) Estimating Gain

(1) and (2) are both based in the gain loss relative to the peak gain. but what is the peak gain? Again there's a simple way to estimate this:

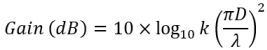
Here the gain is in dBi and k is the efficiency, typically something like 0.65 (65%) for a typical dish with a typical feed and typical edge illumination (ca. -10dB). So this is clearly just an estimate of the gain of an actual dish. Efficiency can range from 50% to 75%, depending in the type of feed, the dish f/D ratio and the resulting edge illumination level.

So for the 3m dish at 1296, assuming an efficiency of 65%, this estimates a gain of 30.3dBi (or 28.15dBd). With an aiming error of 1 degree, gain would drop to (30.3 - 0.41) = 29.89dBi and with an aiming error of 2.7 degrees (1/2 of the full 3dB beamwidth), gain would drop to 27.3dBi.

An Example of use

Suppose I want to know how accurate my tracking system needs to be if I'm using a 1.2m dish at 10.367GHz and I don't want to suffer more than a 1dB loss due to pointing error. Well, fist using equation {1} I estimate the 3dB beamwidth = 70(2.89/120) = 1.7 degrees. Then I use equation {2a} to find the angle at which gain drops by 1dB. That is [SQRT(1*1.7^2)/12] = 0.49 degrees. So to keep gain loss below 1 degree, I have to track with an accuracy of around 0.5 degrees of better. Since the moon moves around 15 degrees/hour, if I'm tracking manually, that means I need to peak the antenna on the moon (using moon noise maybe) at least every 2 minutes. If I aim 0.5 degrees ahead of the moon, I can wait 4 minutes before moving it and lose no more than 1dB of gain during that time.

Recalculating for no more than a 0.5dB gain loss, aiming accuracy should be within 0.36 degrees or better. For no more than 0.25dB gain loss, this tightens up to around 0.25 degrees. Remember that point accuracy depends on a combination of calibration, rotator step-size and backlash in the gear system.

Example #2 - which is better, a small dish pointed accurately or a big dish pointed with a small error?

Let's look at a 1m, a 2m and 3m diameter dish used at 10368MHz. Is it better to point the small dish very accurately, or a larger dish with several degrees of pointing error? I'll use a 0.56 degree pointing error since it gives round numbers for the gain loss.

Note that the 3dB beamwidth is the full beamwidth. An aiming error of 1/2 this value (on either side of the peak) gives a 3dB drop in gain.

Dish
diameter		 3dB full
Beamwidth		 Full Gain
(dBi)		 Gail loss with
0.56 deg error		 Gain (dBi) with
0.56 deg error
1m 2 deg 38.8 1 37.3
2m 1 deg 44.9 4 40.9
3m 0.65 deg 48.8 9 39.4

Example 3 10Ghz dishes

This is a table for 10.368Ghz. The dish is assumed to have 65% efficiency. The numbers should be rounded off to 1 decimal place (at best)

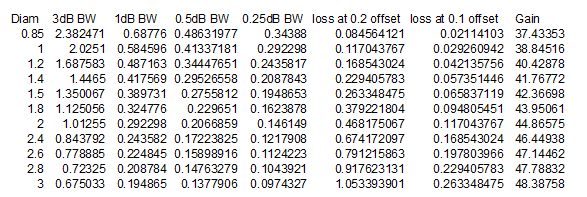
The columns (left to right) are:

(1) Dish diameter (m). For an elliptical offset fed dish use the smaller (horizontal) diameter
(2) The 3dB beamwidth (degrees)
(3) The 1dB beamwidth (degrees)
(4) The 0.5dB beamwidth (degrees)
(5) The 0.25 degree beamwidth (degrees)
(6) The loss with a 0.2 degree aiming error
(7) The loss of gain with a 0.1 degree aiming error
(8) The nominal dish gain (dBi)

As you can see, pointing errors are more costly with a larger dish, and can even rise to the level that results in a larger dish giving lower gain! Clearly if you use a large dish with a narrow beamwidth, you need accurate aiming. What many large dish users do is to use moon noise to optimize pointing rather than depending on the mechanical precision of a tracking system. An AZ EL tracking system may be used, but with the ability to fine tune the position based on moon noise measurements. You'd expect about 0.2dB moon noise with a 1m dish, 0.75dB with a 2m dish and 1.4dB with a 3m dish.

Again I should emphasize that these are just estimates, based on a typical dish with a typical feed (ca. 65% efficient) and typical edge illumination levels found in EME operation (ca. -10dB).

Additional Resources and Reading

Acknowlegements

Thanks to the Moon-net online community for pointing me in the right direction in both public posts and private email. This page is a distillation of the information that they provided. Any mistakes here are all mine!