Signal to noise vs. Signal+noise to noise rations
When you are listening to a signal, you are really listening to that signal plus the background noise, If you then measure the power in the signal+noise and compare it to the power of the noise, you aren't measuring the signal to noise ratio (SNR). You are measuring the (signal+noise) to noise ratio. These are not the same number and the weaker the signal, the more difference there is.
Why is this important? Well, if you measure a signal that has a 30dB (S+N)/N ratio and you lower the signal strength by 3dB, you will get something that shows a (S+N)/N value very, very close 27dB. On the other hand, if you start out with a (S+N)/N ratio of 2dB and you lower the signal power by 3dB you don't end up with an (S+N)/N ratio of -1dB! If there's no signal there at all, your minimum (S+N)/N ratio is 0dB.
If you use signal level to measure something like the -3dB point of an antenna pattern, you want to be measuring at the point where the actual signal strength drips by 3dB, not where the (S+N)/N drops by 3dB and most measurements you are likely to make will be (S+N)/N. Fortunately the two can be converted into each other.
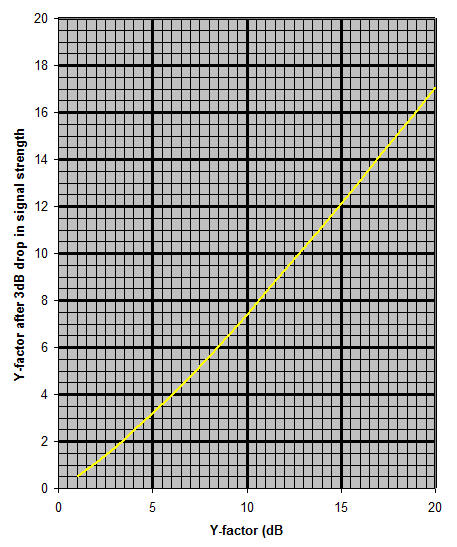
Below is a plot of the (S+N)/N values when the signal (S) drops by 3dB. The ratio of two (S+N)/N is often called the Y factor and in this case it's usually measured as is the difference in dB between the noise (cold sky for example) and the signal+noise (sun noise for example). You can see from the data below that for a 20dB Y-factor, 3dB down is very close to 17dB (17.04db), while for a 1dB Y-factor, a 3dB signal drop gives you a Y-factor of about 0.5dB (0.54dB), not -2dB!
The first plot shows the values for a 3dB power drop
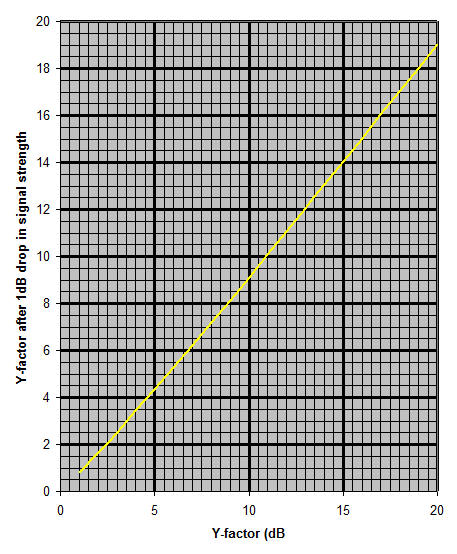
The second plot shows the values for a 1dB drop
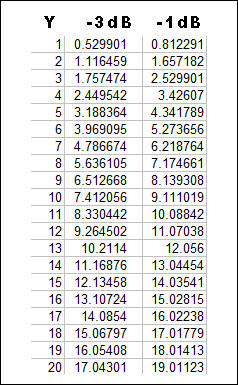
The table shows exact values for 1dB and 3dB power drops for Y-factors from 1dB to 20dB
The Math
It's easier to work with powers and ratios in linear units, not dB, so 20dB=100, 10dB=10, 3db=2 etc.
Y-factor power ratio = 10^(Y-factorDB)/10
(S+N)/N = Y-factor power ratio
S/N + N/N = Y-factor power ratio
S/N + 1 - Y-factor power ratio
S/N = Y-factor power ratio - 1
So now you have the actual S/R ratio. If you start with a Y-factor of 20dB = 100, then S =99. If you want to reduce S by 3dB, S would become 99 * 10^0.3 = 49.62 and so on for other power reductions. So now you can go back the other way and convert this new S value into the (S+N)/N you would see on a dB scale.
S/N = 49.62/1 = 49.62
(S+N)/N = 50.62/1 = 50.62
(S+N)/N (dB) = 10*log(50.62) = 17.04
If you want to wrap this all up into a single formula, here it is:
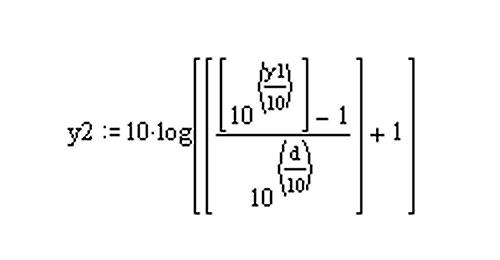
where
y1= original Y-factor reading ((S+N)/N)
d=decrease in signal strength
y2= new y-factor after signal drops by d dB
Alternatively, if y1 and y2 are known, then you can solve for d using:
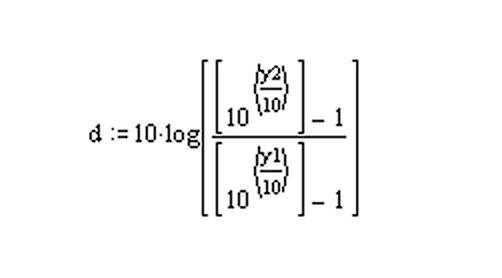
.jpg)