

Digital Depth of Field
Here are the answers
|
• For an equivalent field of view, a Canon APS-C crop sensor camera has at least 1.6x MORE
depth of field that a 35mm full frame camera would have - when the focus distance is
significantly less then the hyperfocal distance (but the 35mm format needs a lens with 1.6x
the focal length to give the same view). • Using the same lens on a Canon APS-C crop sensor camera and a 35mm full frame body, the a Canon APS-C crop sensor camera image has 1.6x LESS depth of field than the 35mm image would have (but they would be different images of course since the field of view would be different) • If you use the same lens on a Canon APS-C crop sensor camera and a 35mm full frame body and crop the full frame 35mm image to give the same view as the APS-C crop image, the depth of field is IDENTICAL • If you use the same lens on a Canon APS-C crop sensor camera and a 35mm full frame body, then shoot from different distances so that the view is the same, the Canon APS-C crop sensor camera image will have 1.6x MORE DOF then the full frame image. • Close to the hyperfocal distance, the Canon APS-C crop sensor camera has a much more than 1.6x the DOF of a 35mm full frame camera. The hyperfocal distance of a Canon APS-C crop sensor camera is 1.6x less than that of a 35mm full frame camera when used with a lens giving the same field of view. |
Now on to the question...
Depth of Field - What it is and what it isn't
Let's try to define depth of field. The usual definition runs something like this:
"The region over which objects in an image appear sharp".
While there is some truth in this, there's also some confusion - and some untruth too! Let's try a more accurate definition:
"The depth of field is the range of distances reproduced in a print over which the image is not unacceptably less sharp than the sharpest part of the image".
This definition contains some important points.
- First, DOF relates to a print or other reproduction of an image. It's NOT an intrinsic property of a lens. If you put a lens on an optical bench you can measure focal length, you can measure aperture, but you can't measure depth of field. Depth of field depends on some subjective factors which I'll discuss later.
- Second, note the phrase "not unacceptably less sharp". All parts of an image which come from outside the focal plane of the lens are blurred to some extent. Only one plane is in focus. As you move away from that plane things get less sharp. The depth of field limits are where the loss of sharpness becomes unacceptable - to a "standard" observer.
- Third, note the phrase "..not unacceptably less sharp than the sharpest part of the image...". This covers the case of a pinhole camera. Such a camera has a very, very large depth of field (almost, but not quite infinite). However none of the image is sharp. The depth of field is large because all the image is equally blurred!
An important thing to note is that depth of field is NOT what some people think it is, i.e. a well defined zone over which everything is in sharp focus. Some people seem to have the impression that an image has two zones. In focus and out of focus. In fact there is only one point (actually plane) in focus. Everything else is out of focus to some extent.
Depth of field is also NOT directly related to background blur. Depth of field equations tell you over what range of distances objects will appear to be acceptably sharp (or at least not unacceptably unsharp). It tells you nothing about how much blur there will be of objects well outside the depth of field. That's governed by different physical parameters and determined using totally different equations, and it's something I intend to address in a future article.
Circle of Confusion - it's confusing
Let's take a look at sharpness and try to make some calculations. Let's take an 8x12 print and look at it from a normal viewing distance of 15". How sharp does it need to be? How large can a point be before it looks like a small disk rather than a point? Obviously this differs from person to person, but a typical value might be 250 microns - which is 1/4 mm or 1/100". OK, so for our purposes, a 250 micron diameter spot is equal to a point in the 8x10 print. What size does this represent in the original image (slide, negative or digital sensor surface)? Well obviously it depends on how much we have to magnify our original image in order to get an 8x12 print.
For example if we are enlarging a 35mm negative (24mm x 36mm) to an 8" x 12"
print we have to magnify it by a factor of 8.46. So the size on the negative that would
give a 250 micron spot on the print is 250/8.46 microns, or 29.5 microns. This is the well
known as "circle of confusion" value. It's the largest spot on the
original image which may still look like a point (rather than a disk) in the print. So we
have a circle of confusion value of 29.5 microns for 35mm, and indeed this is close to the
number (30-35 microns) often used for 35mm DOF calculations. Now you know why! Below is a
table showing corresponding numbers for a sensor the size of that used in the EOS
10D and in a nominal 6x9 medium format camera (most 6x9 cameras have a smaller negative
size, around 56 x 84 mm, but let's ignore that for now).
| Camera | Format Size (nominal) | Magnification needed to make 8" x 12" print | Spot size needed to give 250 micron spot
in print = "circle of confusion" |
| APS-C Crop sensor | 15 x 22.5 mm | 13.55x | 18.45 microns |
| 35mm full frame | 24 x 36 mm | 8.46x | 29.5 microns |
| 6x9 | 60 x 90 mm | 3.38x | 73.96 microns |
One thing to note here is that for these numbers to have any real meaning with respect to depth of field, the circle of confusion value must be larger than the smallest element the film or digital sensor can resolve. For example, the pixels on the 10D are about 7.4 microns square, so the use of a circle of confusion value of 18.45 microns is reasonable. Film can resolve detail down to less than 5 microns, so the film numbers are good too, For reference 1 micron is 1/1000000 meter or 1/1000 mm.
Note also that we have made assumptions about print size, viewing distance and visual acuity in these calculations. These happen to be the "standard" assumptions most camera makers make when calibrating the depth of field scales on their lenses. If we were looking at 4x6 prints from a distance of 6ft, or a 100ft x 150ft billboard from a distance of 3ft, we'd need to make a whole new set of assumptions and we'd calculate totally different values for the circle of confusion and so we'd have a totally different depth of field scale. So just to drive this point home, depth of field depends on the size of the print, the viewing distance and how good your eyes are. The "standard" depth of field scales assume something like an 8x10 (or 8x12) print viewed at a distance of around 15" by someone with average eyesight.
Format related Depth of Field
Since I don't want to scare readers way with a page of algebra showing the derivation of the following equation, I'll just state it. You can derive it (as I did) from the simple lens equation - or you can just take my word for it!
![]()
Here F is the focal length. D is the subject distance, c is the circle of confusion and fn is the f# (f-stop) of the lens. Now this equation doesn't reduce to some simple rule of thumb. However we can say that over the range of focus distances which aren't in the macro range (where D is close to F) and which aren't close to the hyperfocal distance (where D = F*F/fn*c) you can "guesstimate" that the depth of field ratio between two lenses used at the same aperture and focused at the same distance by assuming it's proportional to the size of the circle of confusion and inversely proportional to the square of the focal length.

Again, this simple analysis only applies at "intermediate" distances, but we have to have that limitation if we want a "simple" formula. It only really breaks down when the lens is focused further than about halfway to the hyperfocal distance or when we get to magnifications near 1:1
Now I think we all know that to get the same field of view on different format cameras we need different focal length lenses. Most people by now know that a Canon APS-C crop sensor camera has a 1.6x "multiplier", meaning that a lens designed for use on a 35mm full frame camera when used on a Canon APS-C crop sensor camera gives you the same field of view as a lens 1.6x longer on a conventional full frame 35mm camera. So a 50mm lens when mounted on a Canon APS-C crop sensor camera gives you the same field of view as you would get with a (50x1.6) = 80mm lens on a 35mm full frame body.
| Camera | Format Size | Relative Size (focal length "multiplier") | Lens giving same view as 50mm on 35mm |
| APS-C Crop Sensor | 15 x 22.5 mm | 0.625 (1.6x) | 31.25mm |
| 35mm Full Frame | 24 x 36 mm | 1.0 (1x) | 50mm |
| 6x9 | 60 x 90mm | 2.5 (0.4x) | 125mm |
OK, so now I think we are finally in a position to figure out
what the relative depth of field will be for different formats! We could do it by algebra,
but for the math-phobic let's just do it by considering a few examples:
| Camera | COF | Focal length | Value of COF/(focal length)^2 | Relative DOF |
| APS-C Crop Sensor | 18.45 | 31.25 | .019 | 1.6 |
| 35mm Full Frame | 29.5 | 50 | .012 | 1 |
| 6x9 | 73.96 | 125 | .00473 | 0.4 |
So the bottom line - and all you really need to know - is that DOF is inversely proportional to format size. Note that format size is inversely proportional to the "digital multiplier". The higher the "digital multiplier", the smaller the format and thus the greater the depth of field. Note also that now you can see one of the reasons large format camera users need tilts and swings to get adequate depth of field. With an 8x10 camera you have about 8.5 times LESS depth of field than you do with 35mm for the same image. This also explains why consumer digicams, some of which have sensors 1/6 the size of 35mm film, have such a large depth of field and one of the reasons why it's almost impossible to get blurred backgrounds when using them.
So if you make the same size print and shoot with a lens that gives you the same view and you use the same aperture, if you halve the format size you double the DOF, if you double the format size you halve the DOF. Pretty easy to remember eh? The 1.6x "digital multiplier" for lenses corresponds directly to a 1.6x "DOF multiplier" when comparing the Canon APS-C crop sensor camera to 35mm when you use lenses with the same angle of view.
I'm sure some people will say, OK, but what if you don't take angle of view into account. What's the relative DOF if you use the SAME lens on a Canon APS-C crop sensor camera and a 35mm full frame body?
Now you run into the problem of what you are comparing to what. The same lens on the two formats will give you different fields of view, so if you enlarge each image to the same size (say 8x12), you won't have the same print so you really can't compare DOFs. If you crop the 35mm negative to give you the same print as the digital image the answer is easy. The DOF in the cropped 35mm print and digital image print will be exactly the same. You're using the same lens and same size image (cropped 35mm or digital), so you get exactly the same DOF.
What if you don't crop? Well, you have different views, but you can still compare DOF I guess. The focal length of the lens is the same in each case, so the ratio of the DOFs is just the ratio of the circle of confusion values, 18.45 microns for the Canon APS-C crop sensor camera, 29.5 microns for the 35mm full frame. The ratio is 1.6x - there's that number again! The Canon APS-C crop sensor camera image now has less 1.6x DOF than 35mm - but note that it still has at least 1.6x more DOF than the 35mm full frame would have if an 80mm lens had been used with the full frame camera to give the same field of view as the 50mm lens on a Canon APS-C crop sensor camera. The table below shows some typical numbers.
| Camera | Focal Length (mm) | Diagonal Angle of View | f-stop | Focus Distance (mag) |
Hyperfocal distance | Near point of DOF | Far point of DOF | Total DOF | Relative DOF |
| Data below are for a close-up condition | |||||||||
| APS-C | 31.25 | 46° | f8 | 0.15m (.26x) | 6.6m | 0.147m | 0.153m | 5.39mm | 1.9 |
| APS-C | 50 | 29° | f8 | 0.15m (.5x) | 16.9m | 0.1491m | 0.1509m | 1.77mm | 0.6 |
| 35mm | 50 | 46° | f8 | 0.15m (.5x) | 10.6m | 0.1486m | 0.1515m | 2.83mm | 1.0 |
| 6x9 | 125 | 46° | f8 | 0.15m (5x) | 26.4m | 0.1498m | 0.1501m | 0.237mm | 0.08 |
| Data below are for an intermediate condition (not macro, not close to HFD) | |||||||||
| APS-C | 31.25 | 46° | f8 | 2m | 6.6m | 1.54m | 2.85m | 1.31m | 1.7 |
| APS-C | 50 | 29° | f8 | 2m | 16.9m | 1.79m | 2.26m | 0.47m | 0.6 |
| 35mm | 50 | 46° | f8 | 2m | 10.6m | 1.69m | 2.45m | 0.76m | 1.0 |
| 6x9 | 125 | 46° | f8 | 2m | 26.4m | 1.87m | 2.15m | 0.28m | 0.4 |
Data below are for focus distance close to hyperfocal distance for a 31.25mm lens on a Canon APS-C crop sensor camera |
|||||||||
| APS-C | 31.25 | 46° | f8 | 5m | 6.6m | 2.85m | 20m | 17.15m | 2.85 |
| APS-C | 50 | 29° | f8 | 5m | 16.9m | 3.9m | 7.1m | 3.2m | 0.53 |
| 35mm | 50 | 46° | f8 | 5m | 10.6m | 3.4m | 9.4m | 6m | 1.0 |
| 6x9 | 125 | 46° | f8 | 5m | 26.4m | 4.2m | 6.1m | 1.9m | 0.32 |
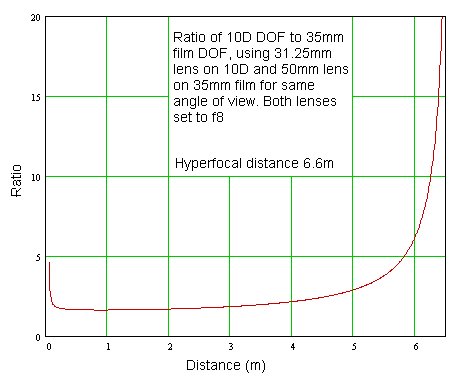
Note that as the focus distance approaches the hyperfocal distance, DOF increases rapidly. Since this happens for the a Canon APS-C crop sensor camera with a 31.25mm lens first (because the hyperfocal distance is least), the ratio of the DOF of the a Canon APS-C crop sensor camera to that of 35mm full frame becomes larger than the ~1.6x that you would get if the lens was focused at a distance much shorter than the hyperfocal distance. The plot below shows this graphically. Between about 0.2m and 3m the Canon APS-C crop sensor camera shows about 1.6-1.7x the DOF of 35mm full frame. At very close distances the ratio goes up, and as the distance approaches the hyperfocal distance for a 31.25mm lens at f8 on a Canon APS-C crop sensor camera (6.6m) the ratio rapidly rises - this is because the DOF behind the subject in the Canon APS-C crop sensor camera image is rapidly moving towards infinity.
I suppose you are now totally confused - even I'm getting confused - too many numbers and too many examples! So I'll just summarize the results and you can forget the explanation!
|
• For an equivalent field of view, a Canon APS-C crop sensor camera has at least 1.6x MORE
depth of field that a 35mm full frame camera would have - when the focus distance is
significantly less then the hyperfocal distance (but the 35mm format needs a lens with 1.6x
the focal length to give the same view). • Using the same lens on a Canon APS-C crop sensor camera and a 35mm full frame body, the a Canon APS-C crop sensor camera image has 1.6x LESS depth of field than the 35mm image would have (but they would be different images of course since the field of view would be different) • If you use the same lens on a Canon APS-C crop sensor camera and a 35mm full frame body and crop the full frame 35mm image to give the same view as the APS-C crop image, the depth of field is IDENTICAL • If you use the same lens on a Canon APS-C crop sensor camera and a 35mm full frame body, then shoot from different distances so that the view is the same, the Canon APS-C crop sensor camera image will have 1.6x MORE DOF then the full frame image. • Close to the hyperfocal distance, the Canon APS-C crop sensor camera has a much more than 1.6x the DOF of a 35mm full frame camera. The hyperfocal distance of a Canon APS-C crop sensor camera is 1.6x less than that of a 35mm full frame camera when used with a lens giving the same field of view. |
I think this is where we came in...
ADDENDUM
As the result of discussions of this article I've added the following comments on the use of DOF scales on lenses.
Many prime lenses have Depth of Field scale markings. These enable an estimate of DOF to be made based on focusing distance and aperture. Below is an example. This is a 17mm lens with a DOF scale designed for use on a full frame 35mm film camera. The aperture is set to f16 and the focus is set to 0.7m. Opposite the f16 marking on the right you can see a distance of infinity is indicated and opposite the f16 marking on the left you can see a distance of something less than 0.4m is indicated. So when this lens is used at f16 and focused at 0.7m, the depth of field extends from just less than 0.4m to infinity.

Now let's look at the case when this lens is used on a Canon APS-C crop sensor camera. As the article indicates, if you use a given lens on a smaller format, depth of field is reduced and the angular coverage ("effective 35mm equivalent focal length) decreases. In the case of a Canon APS-C crop sensor camera it's reduced by a factor of 1.6, so it gives the same angular coverage (field of view) as a 27mm lens on a full frame 35mm body. The circle of confusion value for the Canon APS-C crop sensor camera is reduced by a factor of 1.6x and what this means in terms of DOF scales is that you need to use the markings for about 1 1/3 stops wider aperture in order to estimate the DOF. So with the lens set to f16, we need to look at the DOF scale markings about 1/2 way between f8 and f11 as shown below. In this case, if we want infinity to be at one end of the depth of field, we have to focus at 1m. This gives us a DOF extenting from just over 0.5m to infinity.

Note that the numbers quoted above are approximate. They aren't quite the same as you'd get from a detailed DOF calculation, but that's because you can't read the DOF and distance scales on a lens accurately to two decimal places, plus you don't know quite what value the manufactuer used for the circle of confusion value (it's usually between 30 and 35 microns).
