

Field of View - Rectilinear and Fishye Lenses

Left: Fisheye Right: Rectilinear conversion from fisheye
With the advent of digital cameras having non-standard sensor sizes there seems to be quite a lot of confusion concerning focal length, field of view and digital multipliers and how they relate. This article is intended to try to clear up some of that confusion.
First let's define a few terms:
Focal length: The focal length of a lens is defined as the distance from the optical center of a lens (or, the secondary principal point for a complex lens like a camera lens) to the focal point (sensor) when the lens is focused on an object at infinity. It's a primary physical characteristic of a lens which can be measured in an optical lab. It remains the same no matter what camera the lens is mounted on. A 7mm focal length lens is always a 7mm focal length lens and a 300mm focal length lens is always a 300mm focal length lens
Field of View: The field of view of a lens (sometimes called the angle of coverage or angle of view) is defined as the angle (in object space) over which objects are recorded on the film or sensor in a camera. It depends on two factors, the focal length of the lens (see above) and the physical size of the film or sensor. Since it depends on the film/sensor size it's not a fixed characteristic of a lens and it can only be stated if the size of the film or sensor it will be used with is known. For a lens used to form a rectangular frame, three fields of view are often given; the horizontal FOV, the vertical FOV and the diagonal FOV
Digital multiplier: Digital multiplier is a term that's come into use with the increased use of digital cameras with a sensor smaller than the frame size of a 35mm camera. Since the angle of view of a lens depends on both the focal length of the lens and the size of the image you can define a "digital multiplier", which is the factor by which a lens's focal length would have to be increased to give the same angle of view was the lens has on a digital sensor. For example, a 100mm focal length lens mounted on a digital camera with a "1.6x" multiplier sensor has the same field of view on that camera as a 160mm lens would have when mounted on a full frame 35mm camera. It's still a 100mm focal length lens, but it acts like a 160mm lens would on a full frame camera.
What we're really most interested in from a photographic viewpoint is the Field of View. If we want a wideangle shot we want a wide field of view (say, 84 degrees horizontal). If we want a "normal" shot we want a "normal" field of view (say, 40 degrees horizontal) and if we want a telephoto shot, we want a narrow field of view (say 6.5 degrees horizontal). For those used to thinking in terms of 35mm cameras these would correspond to lenses with focal lengths of 20mm, 50mm and 300mm respectively. However for 4x5 camera users, they'd think in terms of a wideangle 80mm lens, a 200mm normal lens and a 1200mm telephoto lens. So again, FOV isn't determined by focal length, it's defined by focal length AND format size. That's why when we come to APS-C format digital SLRs (with a sensor approximately 15mm x 22mm) the wideangle lens is now 12.5mm, the normal lens is now 32mm and the telephoto lens is now 188mm. Note that these number are the same as the 35mm numbers divided by a "1.6x digital multiplier" (or in this case, a "1.6x digital divider").
Rectilinear and Fisheye Lenses
There are two types of lens you'll find in photographic use.
The first is the rectilinear lens, This is the typical lens which renders all straight lines in the subject as straight lines in the image (see diagram below). It's pretty much the way our eyes see things and it's exactly the way a pinhole cameras sees things. For normal and telephoto use, a rectilinear lens is ideal, however for extreme wideangle use it isn't. Objects near the edges of the frame in very wideangle shots are "stretched". It's also impossible to make a rectilinear lens with 180 degree (hemispheric) coverage. In fact it's very difficult to make a rectilinear lens with more than about 100 degrees of horizontal coverage
The second type of lens is the fisheye lens. A fisheye lens renders straight lines which don't run through the center of the frame as curved (though lines running through the center remain straight). Objects at the edges of the frame are not stretched, but they are distorted. It's easy to make a lens with a diagonal coverage of 180 degrees ("full frame fisheye") or even with a horizontal, vertical and diagonal FOV of 180 degrees ("circular frame fisheye") - though this results in a circular image with the rest of the frame dark. Fisheye lenses were first made for scientific use, since with hemispherical coverage they can image the entire sky on a single frame and so were useful for astronomical and meteorological studies. The first "fisheye" camera was a pinhole camera that was filled with water, but luckily technology has come up with more convenient ways to make fisheye images!
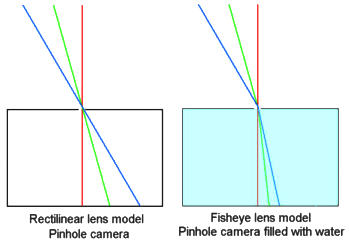
The illustrations above show the pinhole model of rectilinear and fisheye lenses. In a fisheye lens wide angle rays are bent in more towards the center of the frame. To do this with real lenses a very large, very strongly curved negative front element must be used as shown in the lens diagrams below:
Calculating Field of View
Rectilinear Lenses
The field of view of a rectilinear lens focused at infinity is very easy to calculate using simple trigonometry. It's given by:
FOV (rectilinear) = 2 * arctan (frame size/(focal length * 2))
Here "frame size" refers to the dimension of the frame in the direction of the FOV, so for 35mm (which is 24mm x 36mm), frame size is 36mm for the horizontal FOV, 24mm for the vertical FOV and 43.25mm for the diagonal FOV.
Below is a calculator for FOV in both angular and linear terms. The angular field of view assumes infinity focus, and the linear field of view is also based on that, which isn't technically correct, but as described below the corrections for closer focusing aren't significant until you get into the macro range. The "digital multiplier" is 1.6x for most Canon consumer DSLRs, 1.3x for the EOS 1D, 1x for the EOS 1Ds, 1.5x for most Pentax, Nikon and Sony DSLRs and 2x for most Olympus DSLRs.
As the lens is focused at distances closer than infinity the field of view narrows, but unless you get into the macro range, the change is very small. The corrected forumula is:
FOV (rectilinear) = 2 * arctan (frame size/(focal length * 2 * (m+1)))
Where "m" is magnification. At infinity m=0, so the first formula applies. A 50mm lens focused at infinity has a horizontal field of view of about 39.6 degrees for a full frame 35mm camera. For the same 50mm lens focused at 0.55m the magnification is 0.1 and the field of view narrows to 36.2 degrees, so you can see that even for pretty close focus (0.55m is under 22"), the FOV doesn't change much.
Magnification can be estimated by:
m = (focal length)/(focus distance - focal length)
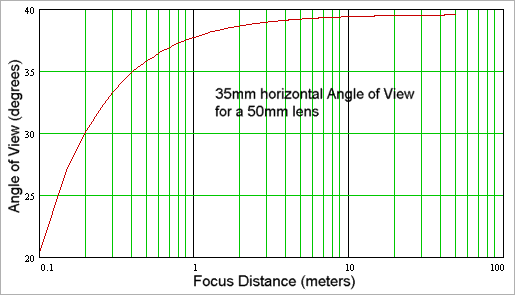
Here's a plot of the horizontal angle of view of a 50mm lens on a 35mm frame as a function of the focus distance. As you can see, the angle of view stays pretty constant until the focus distance gets quite short.
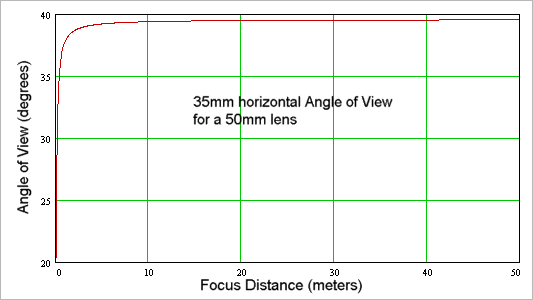
Here's the same plot on a log axis so you can better see how things change at short focus distance:
Fisheye Lenses
The situation is rather more complex for fisheye lenses because there is no such thing as a "Fisheye" equation. Instead there are several different "mapping equations" or "projections" which different fisheye lens manufacturers have used.
Probably the most common is the equisolid angle projection, and the FOV at infinity focus is given by:
FOV (equisolid fisheye) = 4 * arcsin (frame size/(focal length * 4))
Also popular is the equidistance projection, and for the the field of view is given by:
FOV (equidistance fisheye) = (frame size/focal length)*57.3
(the 57.3 is to convert from radians to degrees).
Less common are the orthogonal projection which gives the following field of view:
FOV (orthogonal fisheye) = 2 * arcsin (frame size/(focal length *2)
and the stereographic projection which gives:
FOV (stereographic fisheye) = 4 * arctan (frame size/(focal length * 4))
Of course just like the fact that rectilinear lenses are rarely ever truly rectilinear (they suffer from barrel and pincushion distortion), so fisheye lenses usually don't follow the exact mapping suggested by these equations. This is generally of no consequence unless you are trying to do scientific studies involving precise conversion of points in a fisheye image to "real world" coordinates.
You can think of the various rectilinear and fisheye projections as being somewhat analogous to map projections. We all know the earth is a sphere, but we can represent it on a rectangular map with horizontal and vertical straight lines representing latitude and longitude using a Mercator projection. This could be looked on as an analogy to a rectilinear lens mapping. However just like a rectilinear lens tends to stretch out objects at the edge, such a map projection stretches out areas near the poles. Fisheye lens projection would then correspond to various map projections where latitude and longitude lines are no longer straight, but where, say, areas are proportional, such as azimuthal equal area. Each mapping scheme distorts "reality" in some way. We're more used to seeing one than the other, so with think of one as "normal" and one as "distorted", but that's not strictly true.
The plot below shows how the field of view relates to frame size for a given focal length lens for a rectilinear lens and four types of fisheye lens. As you can see, the rectilinear lens can never get to a 180 degree FOV, no matter how large the frame size, but all the fisheye lenses can. You can also see that for all the lenses, the field of view increases with frame size.
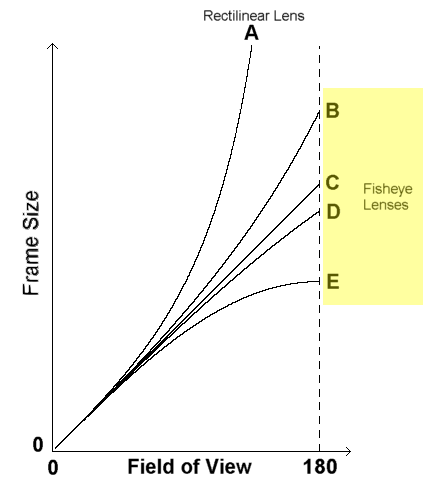
C and D are equidistance and equisolid angle fisheyes respectively (most common)
B and E are stereographic and orthogonal fisheyes respectively (little used)
Note that you can't just take any lens and use a very large frame to get a wide field of view. Lenses have an image circle which is the diameter of the largest image that the lens can form. Outside that diameter the lens vignettes, cutting off the image due to the limited size of the optical elements or other characteristics of the design.. Lenses designed for use on full frame 35mm cameras must be designed to have an image circle of at least 43.5 mm, since the diagonal dimension of the 35mm frame is 43.25mm. It's very difficult to make short focal length lenses with large image circles.
Example
Using the above information we can calculate, for example, the field of view of a full frame fisheye lens designed for 35mm use when used on an APS-C camera. Lets take the example of a 15mm fisheye lens. Let's assume it uses equisolid angle projection, so the FOV is given by 4 * arcsin (frame size/(focal length * 4)).
For a 24 x36mm frame this gives a horizontal FOV of 147.5degrees, a vertical FOV of 94.3 degrees and a diagonal FOV of 185 degrees. Canon give numbers of 142, 92 and 180 for their 15/2.8 fisheye lens, so the mapping isn't exactly equisolid angle, but it's a typical full frame fisheye with approximately 180 degrees diagonal coverage
For a 22.7 x 15.1mm sensor (APS-C) the numbers become: Horizontal FOV = 88.9 degrees, Vertical FOV = 58.3 degrees, diagonal FOV = 108.1degrees. If you "defish" a fisheye image, i.e. convert the image to rectilinear mapping, you keep the horizontal and vertical FOV, stretch the edges of the image and reduce the diagonal FOV. So if you "defished" the image you'd get an image with approximately and 88 degree horizontal FOV and a 58 degree vertical FOV. This corresponds to the horizontal FOV of a 19mm lens and the vertical FOV of a 22mm lens. How is this possible? Well the 1:1.5 ratio of vertical to horizontal if the APS-C sensor is changed when the image is "defished" and becomes closer to 1:1.7

Paint Shop Pro has a built in fisheye to rectilinear conversion function, as do a number of other image editors and stand alone programs.


